قياس بعد وقطر القمر بطريقه بسيطة

كان الإنسان منذ القدم شغوفًا بالسماء من حوله، وتأمل  ما تحويه مِن كواكب ونجوم منذ فجر التاريخ، وطالما كان الإنسان متطلعا إلى أن يعرف أكثر عن تلك الأجرام التي زينت السماء ويراها باستمرار

🔹️كم تبعد عنا على الارض؟

وما هى أحجامها الحقيقية؟

 واليوم يا اصدقائي  بفضل التقدم العلمى الذي وصلنا إليه نستطيع معرفة الكثير من التفاصيل الدقيقة عن الشمس والقمر والنيازك والكواكب القريبه  والكثير من النجوم

وفي هذا المقال نتحدث عن جزء من رحلة المعرفة التي قادت الإنسان عبر الزمن لما وصل إليه اليوم من تقدم علمى بل سنمارس جزءًا من هذه التجربه بأنفسنا وببساطه

سنتعلم كيف يمكننا أن نقيس بعد أقرب جرم الينا على الارض وهو  -القمر- 

بطرق سهلة ومبسطة، ويمكن للجميع القيام بها بسهوله

حركه القمر حول الارض

يتحرك القمر حول الأرض في مدار بيضاوي مما يؤدي إلى تغير المسافة بينهما حسب موقع القمر، لكن متوسط المسافة بينهما قد تم تحديده في 384399 كيلومتر. و لادراك هذه القيمة فهي تقارب عشر لفات حول الأرض في خط الاستواء.

لكن كيف تم قياس هذه المسافة؟

هناك عدة طرق لقياس المسافة بين الأرض و القمر، و تذكر المراجع أن أول من قام بعملية القياس هاته هو Aristarque de Samos (ولد 310 قبل الميلاد و توفي 230 قبل الميلاد)، و ذلك باستخدام ظاهرة خسوف القمر: حيث لاحظ أن ظل الأرض يمكنه أن يحتوي على 3 أقمار، و بالتالي فشعاع الأرض يساوي 3 أضعاف شعاع القمر

لطالما كان تقدير بعد وقطر الأجرام السماوية أمرا صعبًا، لكنّ هذه الأجرام تحتل مساحة معينة من القبة السماوية -وهو ما يعرف بـ: (القطر الزاوي)- وهي نقطة انطلاق مهمة لمعرفة بعد وقطر الأجرام بعد ذلك.

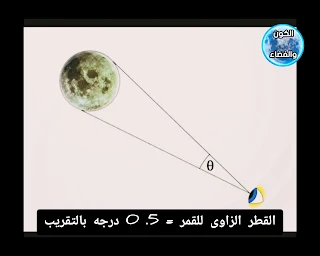
• قياس بُعد القمر:

عَلِم الإنسان منذ القديم أنّ القمر أقرب إلينا من الشمس وأقرب من النجوم، لكن لا زالت المهمة صعبة نوعًا ما، وبالعقل الذي كرم الله الإنسان به استطاع تذليل الصعاب في طريق العلم والمعرفة.

• الطريقة الأولى (طريقة خسوف القمر):

البعد التقريبي للقمر قيس قبل الميلاد، أي: قبل أكثر من ألفي عام، عن طريق علماء الفلك الإغريق.

وكانوا قد أدركوا كروية الأرض، وقاسوا محيطها، ومن ثمّ عرفوا قطرها التقريبي.

وكانت هذه القياسات التي تمكنوا من معرفتها بطرق ذكية هي الأساس الذي مكنهم من معرفة بعد القمر التقريبي بعد ذلك.

• تجربة تمهيدية:

عند الظهيرة، أمسِكْ بيدك قطعة نقدية أو أي جسم دائري وضَعه بالشمس، سيشكل هذا الجسم ظلًا مخروطيًا، حاول أنْ ترفع هذا الجسم وتخفضه حتى يستدق ظله على الأرض تمامًا.

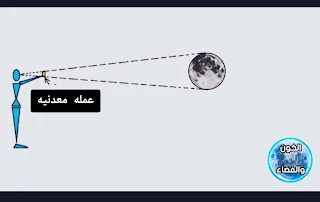
عند هذه النقطة سيساوي ارتفاع القطعة المعدنية عن الأرض (108) أضعاف قطرها.

(يجب تطبيق هذه التجربة عندما تكون الشمس متعامدة على ذلك الموقع).

• تجربة أخرى:                                                                                                                                                  عندما يكون القمر بدرًا.. أغمض إحدى عينيك، وخذ قطعة معدنية وضَعها أمام عينك الأخرى، وأبعدها رويدًا رويدًا حتى تغطي هذه القطعة قرص القمر دون زيادة أو نقصان، حينئذ ستكون المسافة بين عينك وبين القمر تساوي (108) أضعاف قطر هذه القطعة المعدنية.

نفس التجربة السابقة يمكن تطبيقها على الشمس، وسنحصل على نفس النتائج؛ لأن القطر الزاوي لكل من الشمس والقمر متساويان.

ملاحظة: في حالة تنفيذ هذه التجربة مع الشمس يجب أخذ الاحتياطات اللازمة واستخدام النظارات الواقية، لا تنظر للشمس بشكل مباشر أبدًا.

• تفاصيل الطريقة:

يعبر القمر من منطقة ظل الأرض خلال خسوف القمر، لذلك عليه أن يعبر من مسافة أقصاها (108) أضعاف قطر الأرض مهما كان قطر القمر، وخلال الخسوف القمري الكامل عندما يعبر القمر من مركز ظل الأرض لوحظ أنّ ظل الأرض يساوي قطر القمر (2.5) مرة تقريبًا.

لكن هل هو قمر كبير وبعيد، أم أنه قمر صغير وقريب؟!

ربما كان من الصعب معرفة ذلك لولا صدفة أخرى سعيدة، ألا وهي: كسوف الشمس، وخلال الكسوف يغطي القمر قرص الشمس تمامًا دون زيادة أو نقصان.

ومثل تجربة القطعة المعدنية فإنّ ظل القمر يستدق تمامًا على سطح الأرض؛ مما يجعل مخروط ظل الأرض ومخروط ظل القمر يشكلان مثلثين متشابهين؛ وهذا يمكننا من استخلاص كثير من المعطيات من خلال علم المثلثات.

المثلثات:-

أكبرها:

قاعدته = قطر الأرض

وارتفاعه = (108) مرات قطر الأرض

أصغرها:

قاعدته = قطر القمر

وارتفاعه = بعد القمر = (108) مرات قطر القمر

والمتوسط:

قاعدته = (2.5) مرات قطر القمر

وارتفاعه = (2.5) مرات بعد القمر (حسب تشابه المثلثات)

إذن الآن يصبح:

قاعدة المثلث الأكبر= (3.5) قطر القمر

وارتفاعه = (3.5) بعد القمر

والنتيجة:

المسافة إلى القمر تساوي (108) مرات قطر الأرض ÷ (3.5)

ويساوي (1390473) كلم ÷ (3.5)

ويساوي (397,278) كيلومتر

وبحسب القياسات الحديثة فإنّ متوسط المسافة إلى القمر يبلغ (384) ألف كيلومتر

في حين يبلغ بعده في نقطة الأوج (406.700) كيلومتر، وفي نقطة الحضيض (356.500) كيلومتر.

وقطر القمر = قطر الأرض ÷ (3.5)

= (12.742) ÷ (3.5) = (3,640) كيلومتر.

قطر القمر الحقيقي: (3.474) كيلومتر.

أي: إنّ نسبة الخطأ في تقدير قطر القمر أقل من (5%).

– الطريقة الثانية (طريقة التزيح) (اختلاف المنظر):

التزيح: هو تغير ظاهري في موقع الشيء المنظور بسبب اختلاف مكان وزاوية الرؤية.

• تجربة بسيطة:

لفهم التزيح بشكل أوضح.. أمسك قلمًا على طول ذراعك

أغلق عينك اليسرى وانظر له بعينك اليمنى، والآن بدّل بين عينيك، لاحظ كيف يختلف موقعه الظاهري بالنسبة لخلفية المنظر عند تبديل النظر بين عينيك. 🙂

نفس الأمر في التجربة السابقة يحصل بمقياس كبير بالنسبة للقمر، فمراقبان للقمر من موقعين مختلفين يبعدان عن بعضهما مسافة كبيرة سيلاحظان تغيرًا في الموقع الظاهري للقمر، بينما النجوم التي في الخلفية ستبقى كما هي؛ لأنها بعيدة نسبيًا.

لو التقط هذان المراقبان صورة للقمر مع خلفية النجوم المحيطة، ثم طابقنا القمر في الصورتين.. سيصبح لدينا مثلث، قاعدته هي: المسافة بين المراقبين، ورأسه هو: القمر.

طول قاعدته معروفة، وزاوية التزيح يمكن حسابها من خلال الصورة.

وباستخدام النسب المثلثية يمكننا إيجاد طول العمود الواصل من قاعدة المثلث إلى القمر والذي يمثل بُعد القمر.

وتقوم كثير من المؤسسات والجمعيات العلمية بشكل مستمر بتنظيم فعاليات عبر العالم للمشاركة بقياس بعد القمر بهذه الطريقة؛ لتنمية روح البحث وحب علم الفلك لدى الطلاب والمهتمين.

المثال الأول:

وهو مثال لأحد تلك التجارب التي نُظّمت لقياس التزيح خلال خسوف القمر الكلي الذي وقع في الخامس عشر من شهر حزيران (يونيو) عام (2011).

موقعا التصوير للراصدين كانا بين وسط أوروبا من جهة وشرق أسيا وأستراليا من جهة أخرى؛ لضمان أكبر قاعدة ممكنة للمثلث عند قياس التزيح.

كان القمر يشرق بالنسبة للمراقبين من أوروبا ويغرب بالنسبة للمراقبين من آسيا

وطلب من المراقبين أن يظهروا صورة النجوم التي حول القمر، وأن تظهر المعالم القمرية؛ ليتسنى مطابقة الصورتين من أجل قياس التزيح.

النجم الذي قيس تزيح القمر بالنسبة له هو: النجم (51 Ophiuchi).

المراقب الأول من: تشينغداو – الصين.

المراقب الثاني من: أضنة – تركيا.

المسافة بين موقعي المراقبين (المسافة القوسية) تساوي (4549) ميلًا

المسافة المباشرة بينهما: (4303) أميال

وجد أنّ التزيح يساوي: (65.8) دقيقة زاوية، وهو ما يعادل: (1.097) درجة.

الآن، العمود الساقط من رأس المثلث على قاعدته ينصف كل من الزاوية والقاعدة، وينتج مثلثين قائمي الزاوية؛

فتصبح الزاوية: (0.5485) درجة

وطول قاعدة المثلث قائم الزاوية (2151.5) ميلًا

الآن، بحساب المثلثات:

ظل الزاوية = طول الضلع المقابل÷طول الضلع المجاور

إذن:

المجاور = المقابل÷ظل الزاوية

= 2151.5÷0.00957342

=224,737 ميلًا

=361680 كيلو متر

الآن، نضيف المسافة من قاعدة المثلث إلى مركز الأرض، وهي: (3328) ميلًا

=228,065 ميلًا

=367035 كيلومتر

بُعد القمر من سطح الأرض =228,065- 3,958.75 =224,106 ميلا

والآن إذا علمنا المسافة من الأرض للقمر، ولدينا القطر الزاوي للقمر ويساوي (30) دقيقة زاوية أو نصف درجة

القطر الزاوي = (قطر الجرم÷ محيط الدائرة نصف قطرها المسافة إلى ذلك الجرم) × 360

قطر الجرم = (القطر الزاوي÷360) (2 ×3.14×224,106)

= (0.5÷360) (6.18×224,106)

(0.0013888889)(1,384,975.08)

= (1,924) ميلًا.

والقطر الفعلي للقمر: (2159) ميلًا

أي: إنّ نسبة الخطأ في حساب قطره تساوي: (10%) تقريبًا

وكلما تحرينا الدقة في القياسات.. حصلنا على نتائج أدق.

المثال الثاني:                                                                                                                                                     وهو قياس تزيح القمر خلال الخسوف الكلي الذي وقع في شهر تموز الماضي.

الجرم الذي قيس التزيح بالنسبة له هو كوكب المريخ

الصورة الاولى تصوير معاذ عياش، الدمام-السعودية.

الصورة الثانية تصوير محمد برازي، حماة، سوريا.

المسافة القوسية بين حماة والدمام 1560 كلم، المسافة المباشرة= 1556.12 كلم.

القمر قطره الزاوي للقمر وقت الخسوف في 27/07/27 كان0.4934 درجة

بعد دمج الصورتين:

التزيح: 0.222377464788732 درجة.

الآن، بحساب المثلثات كما في المثال السابق:

ظل الزاوية = طول الضلع المقابل÷طول الضلع المجاور

إذن:

طول الضلع المجاور (المسافة إلى القمر) = المقابل÷ظل الزاوية

الزاوية = 0.222377464788732÷2

=0.1111887324

ظل هذه الزاوية=0.00194061

طول الضلع المجاور= 778.06 ÷ 0.00194061

=400,936 كيلو متر

القطر الزاوي = (قطر الجرم÷ محيط الدائرة نصف قطرها المسافة إلى ذلك الجرم) × 360

قطر الجرم= (القطر الزاوي÷ 360) × محيط الدائرة

= (0.4934÷360) (2 ×3.14×400,936)

=3,451 كيلو متر

وبهذا نكون حصلنا في هذه التجربة على بعد وقطر القمر بنسبة خطأ أقل من 1%

– الطريقة الثالثة (قياس بعد القمر عن طريق موجات الراديو):

وتعتمد هذه الطريقة على إرسال موجات راديو إلى القمر، ثم حساب الفارق الزمني بين إرسال هذه الموجات وعودتها إلى جهاز استقبال الراصد

وبما أنّ سرعة موجات الراديو معروفة -وتساوي سرعة الضوء (300) ألف كيلومتر/ثانية- يمكن حينها حساب المسافة من الأرض إلى القمر

وهذه الطريقة يعرفها جيدًا هواة التواصل باللاسلكي، وتسمى: “Moon bounce” أو: “EME ” (Earth-Moon-Earth)

ويستخدمونها للاتصال ببعضهم البعض